- varianta
- Să se scrie un fişier M în care:
- Să se creeze un vector V cu elementele 15,18,21, ...,96;
- Să se creeze un vector V1 având ca elemente puterea a treia a elementelor din V;
- Să se calculeze suma elementelor din V(S);
- Să se construiască o matrice cu 4 coloane şi 7 linii, conţinând elementele din V (nu prin scriere directă): M=
15 18 21 24 27 30 33 35 . . . . - Să se construiască matricea construită înmulţind element cu element, elementele din M cu elementele din B, unde B =
(4 coloane şi 7 linii);
2 2 2 2 2 2 2 2 . . . . - Să se calculeze rădăcinile polinomului care are ca şi coeficienţi primele 5 elemente din V (considerate de la gradul mai mare);
- Să se calculeze
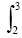 lnxdx.
lnxdx.
- Să se scrie o funcţie în MATLAB care are ca date de intrare o matrice patratică A şi un vector V de aceeaşi lungime cu dimensiunea lui A. Funcţia va returna o valoare x calculată astfel x:=1 daca pe fiecare linie a matricii A, toate elementele sunt mai mari decât elementul din V având acelaşi rang cu rangul liniei lui A şi 0 în caz contrar. Funcţia semnala eroare dacă matricea A nu este pătratică şi va da mesajul: „Matricea nu e pătratică”. De asemenea va fi semnalată eroare dacă lungimea lui V nu e aceeaşi cu dimensiunea lui A, cu mesajul „Dimensiuni necomppătrabile”.
- Să se reprezinte în două subgrafice diferite, dispuse unul sub altul, funcţiile y = sin x şi y = cos x, pentru x ∈ [-2Π,2Π]. O funcţie va fi desenată cu roşu, cealaltă cu albastru.
- varianta
- Să se scrie un fişier M în care:
- Să se creeze vectorul W cu elementele: W = 1,5,9,13, …,37;
- Să se evalueze valoarea polinomului care are aceşti coeficienţi pe punctul x = 5.6;
- Să se construiască din blocuri matricea: A=
1 0 0 0 1 0 1 0 0 1 1 1 1 1 1 1 1 1 1 1 - Să se calculeze suma elementelor din matrice (S);
- Să se înmulţească matricea A cu transpusa ei;
- Să se extragă din această matrice o submatrice formată din primele 3 linii şi primele 3 coloane şi apoi să se scrie elementele acestei matrici sub formă de şir;
- Fie U format din 10 elemente aleatoare situate între [0,10]. Să se calculeze maximul şirului.
- Să se scrie o funcţie în MATLAB, care să aibă ca date de intrare trei vectori de numere reale şi returnează o valoare x, definită astfel: x =1 dacă toate elementele din vectorul de intrare V3 sunt mai mari sau egale decât diferenţa dintre cel mai mic multiplu comun şi cel mai mare divizor comun al mulţimilor astfel pe aceeaşi poziţie în V1 şi V2. Vectorii V1 şi V2 trebuie să aibă aceeaşi lungime, şi funcţia va returna eroare atunci când această condiţie nu e satisfăcută.
- Să se reprezinte în două subgrafice diferite, situate unul alături de altul, funcţiile y = ex şi y = log x, pentru x ∈ [0.1,20]. O funcţie va fi desenată cu negru, cealaltă cu roşu.
- varianta
- Să se scrie un fişier M în care:
- Să se construiască un vector cu 50 de elemente egale cu 1 (V);
- Să se construiască vectorul cu 50 de elemente: W = 1/10; 1/20; …
- Să se contruiască matricea cu 10 linii şi 5 coloane: M=
1 2 3 4 5 6 7 8 9 10 . . . . . - Să se calculeze matricea M1 având ca elemente, elementele din M ridicate la puterea a 2-a;
- Să se calculeze suma elementelor de pe prima coloană a matricii M;
- Să se calculeze:
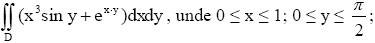
- Să se calculeze valoarea pe punctul x = 5 a polinomului având ca şi coeficienţi primele 4 elemente din W.
- Să se scrie o funcţie în MATLAB care să aibă ca valori de intrare un vector V şi o valoare "a" şi să returneze o valoare "b" calculată astfel : se consideră polinomul care are ca şi coeficienţi elementele vectorului V, începând de la stânga la dreapta cu gradul mai mare şi polinomul care are ca şi coeficienţi elementele vectorului V începând de la dreapta la stânga cu gradul mai mare. Se evaluează aceste polinoame pe punctul "a". Fie valorile obţinute V1 şi V2. Dacă V1 > V2 atunci b=1. Dacă V1 < V2, atunci b = 2. Funcţia va afişa şi un mesaj de forma "S-a: gasit b = ....".
- Să se reprezinte pe acelaşi grafic funcţiile y = sin x, y = cos x, pentru x ∈ [0,2Π]. O funcţie va fi reprezentată cu linie continuă albastră, cealaltă cu linie întreruptă roşie.
- varianta
- Să se scrie un fişier M în care:
- Să se creeze o matrice având 5 linii şi 4 coloane şi elementele: M=
2 4 6 8 10 12 14 16 . . . - Să se calculeze logaritmul zecimal al elementelor matricii M;
- Să se calculeze suma elementelor de pe prima linie a matricii M;
- Să se construiască un vector V care conţine în ordine, linie după linie elementele submatricii din M formată din primele 2 linii şi primele 2 coloane (matricea M1). Fie V acest vector.
- Să se calculeze derivata pe punctul x = 2 a polinomului care are ca şi coeficienţi elementele din V;
- Să se calculeze
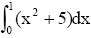 prin metoda Simpson;
prin metoda Simpson; - Să se calculeze cel mai mare divizor comun al primelor 2 elemente din V.
- Să se creeze o matrice având 5 linii şi 4 coloane şi elementele: M=
- Să se srie o funcţie în MATLAB, care să aibă ca date de intrare o matrice patratică A şi să returneze o valoare x definită astfel : x = 1 dacă există în matricea A un element mai mare decât maximul dintre suma elementelor de pe diagonala principală li suma elementelor de pe diagonala secundară şi x = 0 în caz contrar. Funcţia va semnala eroare dacă matricea A nu este pătratică, semnalând mesajul "Matricea de intrare nu este pătratică".
- Să se reprezinte grafic în 3 ferestre aflate una sub alta funcţiile f(x) = x2 cos x , g(x) = x ex şi în ultima fereastră se va reprezenta o sferă unitate, folosind 30 de cercuri pentru reprezentare.
- varianta
- Să se scrie un fişier M în care:
- Să se creeze din blocuri matricea: M=
2 2 2 0 2 2 2 0 0 1 0 0 0 1 0 0 - Să se calculeze suma elementelor matricii A;
- Să se genereze vectorul V = [4,14,24,…,104];
- Să se ridice elementele din vectorul V la puterea a 3-a;
- Să se calculeze valoarea pe punctul x=1 a polinomului având ca şi coeficienţi elementele de pe poziţiile impare ale vectorului V;
- Să se construiască vectorul V1, având elementele din matricea A luate coloană după coloană;
- Să se calculeze
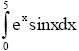 prin metoda Simpson.
prin metoda Simpson.
- Să se creeze din blocuri matricea: M=
- Să se scrie o funcţie în MATLAB care are ca date de intrare două matrici A şi B şi returnează o valoare x calculată astfel: dacă A şi B au acelaşi număr de linii, atunci x este egal cu cel mai mare divizor comun dintre suma elementelor din A şi suma elementelor lui B; dacă A şi B au acelaşi număr de coloane, atunci x este egal cu cel mai mic multiplu comun dintre suma elementelor lui A şi suma elementelor lui B. Dacă A şi B nu au nici acelaşi număr de linii, nici acelaşi număr de coloane, funcţia va semnala eroare şi va scrie mesajul : "Eroare, Condiţie nesatisfăcită"
- Să se reprezinte în două subgrafice diferite, situate unul lângă altul, funcţia y = tan(x),
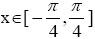 şi o sferă de rază egală cu unitatea.
şi o sferă de rază egală cu unitatea.
Puteti lasa si voi variantele voastre la aceasta materie, in comentariile acestei pagini.






