- Definiti polinoamele lui Bernstein de grad n.
- Definiti polinoamele lui Bernstein de grad n=2, n=3, n=4, n=5.
- Care este valoarea expresiei:
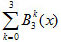
unde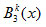 reprezenta polinoamelele lui Bernstein de grad 3.
reprezenta polinoamelele lui Bernstein de grad 3.
- Cum se scrie parametric o curba in plan?
- Cum se scrie parametric o curba in spatiu?
- Cum se scrie parametric o curba in plan, in format Bezier?
- Cum se scrie parametric o curba in spatiu, in format Bezier?
- Exista curbe Bezier (BC) inchise? Justificati raspunsul.
- Exista BC sub forma de segment de dreapta? Justificati raspunsul.
- Schitati cel putin 7 curbe Bezier cubice (BC) cu forme geometrice diferite. Schitati pentru fiecare curba si poligonul de control.
- Ce intelegeti prin conditii de interpolare de tip Lagrange?
- Ce intelegeti prin conditii de interpolare de tip Hermite?
- Ce proprietati de interpolare are poligonul de control al unei curbe Bezier?
- Ce intelegeti prin proprietatea de afin invarianta a unei curbe Bezier?
- Ce intelegeti prin proprietatea de precizie liniara a unei curbe Bezier?
- Se poate reprezenta un cerc complet, folosind o curba Bezier de grad 3? Justificati raspunsul.
- Poate un arc de cerc sa fie reprezentata printr-o curba Bezier cubica? Justificati raspunsul.
- Schitati o Curba Bezier cubica, care are toate punctele Bezier coliniare.
- Desenati poligonul Bezier al unei curbe Bezier cubice (BC) cu un punct de inflexiune.
- Descrieti algoritmul lui de Casteljau. Pentru ce este folosit acest algoritm?
- Scrieti algoritmul lui de Casteljau si structura determinata prin acest algoritm, pentru aflarea punctului de mijloc al unei curbe Bezier cubice
- Scrieti algoritmul lui de Casteljau si structura determinata prin acest algoritm, pentru aflarea punctului corespunzator parametrului t=1/4, al unei curbe Bezier cubice.
- Evidentiati modul de descompunere a unei curbe Bezier cubice, in 2 subcurbe Bezier, folosind algoritmul lui de Casteljau. Unde gasim, in structura determinata de algoritmul lui de Casteljau punctele de control pentru subcurba din stanga, respectiv din dreapta. Ca exemplu practice porniti de la coordonatele a 4 puncte de control oarecare si folositi valoarea t=1/2 pentru algoritmul lui de Casteljau.
- Aplicati algoritmul lui Casteljau pentru determinarea punctelor de control ale unei curbe Bezier cubice care aproximeaza sfertul cercului de raza 1, aflat in primul cadran.
- Care este reprezentarea in MATLAB a formulei de calcul pentru o curba Bezier cubica cu ajutorul polinoamelor Bernstein ? (scrieti formula matriceala).
- Avand date 4 puncte de pe o curba construiti curba Bezier care trece prin aceste 4 puncte. Descrieti etapele necesare pentru determinarea curbei Bezier interpolatoare. Descrieti tehnica de implementare in MATLAB, pentru obtinerea curbei Bezier interpolatoare.
- Ce intelegeti prin infasuratoarea convexa a unei multimi de puncte?
- Enumerati 5 proprietati ale unei curbe Bezier, importante din punct de vedere al geometriei computationale. Justificati raspunsul (importanta proprtietatilor).
- Definiti o curba spline de grad 3 in format Bezier (BSC), formata din 2 curbe Bezier cubice (BC).
- Definiti o curba spline de grad 3 in format Bezier (BSC) formata din trei BC.
- Scrieti algoritmul de calcul a punctelor de control ale unei curbe BC care trece prin 4 puncte digitalizate ale caror coordinate se cunosc.
- Ce proprietate geometrica trebuie sa indeplineasca punctele Bezier vecine punctului de jonctiune a doua curbe Bezier, pentru ca, curba spline Bezier cubica sa fie continua de clasa C0?
- Ce proprietate geometrica trebuie sa indeplineasca punctele Bezier vecine punctului de jonctiune a doua curbe Bezier, pentru ca, curba spline Bezier cubica sa fie continua C1?
- Construiti (desenati) punctele Bezier ale unei curbe spline Bezier cubice(BSC) obtinute prin interpolarea F-Mill a 4 puncte plane necoliniare alese de voi. Descrieti constructia geometrica. Alegeti al doilea si al treilea punct Bezier al ale unei curba spline Bezier (BSC) cubice obtinute prin interpolarea F-Mill astfel incit curba BSC sa nu schimbe curbura (sau sa schimbe curbura).
- Construiti (desenati) punctele Bezier ale unei BSC obtinute prin interpolarea F-Mill a 5 puncte plane necoliniare alese de Dumneavoastra. Descrieti constructia geometrica. Alegeti al doilea si penultimul punct Bezier al BSC astfel incit prima si respectiv ultima BC a BSC sa nu schimbe curbura.
- Definiti parametric o suprafata Bezier bicubica (BS).
- Cate puncte de control sunt necesare pentru calculul unei BS?
- Schitati o BS ale carei curbe de delimitare au cate un punct de inflexiune.
- Schitati o BS care are toate punctele Bezier, cu exceptia unuia, coplanare.
- Schitati o BS care are toate punctele Bezier coplanare.
- Scrieti algoritmul de calcul, (in MATLAB -in format matriceal) pentru aflarea coordonatelor punctelor de pe BS cand se cunosc coordonatele punctelor de control (algoritmul de reprezentarea grafica).
- Scrieti algoritmul de calcul, (in MATLAB -in format matriceal) pentru aflarea coordonatelor punctelor unei suprafete Bezier cilindrice avand ca si curba directoare o curba Bezier cubica, ale carei puncte de control se cunosc.
- Dati exemple de date de intrare care genereaza: o suprafata cilindrica inchisa si o suprafata cilindrica avand curba directoare situata in planul xoy (sau xoz, sau yoz).
- Scrieti algoritmul de determinare, folosind aplicarea produsului tensorial, a punctelor de pe o suprafata BS care interpoleaza 16 puncte digitalizate (date sub forma unor matrice 4x4 de coordinate) si de reprezentare grafica a suprafetei.
- Pentru algoritmul de la pc. 43 dati exemple de date de intare pentru care se obtine: o suprafata simetrica fata de unul dintre planele de coordonate (xoy,xoz,yoz) si o suprafata care trece prin origine.
- Fie f(u,v)=0 reprezentarea parametrica a unei suprafete. Ce obiect geometric se obtine evaluand suprafata, dand unuia din parametri valoarea 0.5 ? Ce rezultat se obtine dand ambilor parametri valoarea 0.5 ? Ce rezultat se obtine dand ambilor parametri valoarea 0 ?
- O BS este simetrica fata de planul de coordonate Oxz. Ce proprietati de simetrie are reteaua Bezier a suprafetei ? Cate din punctele Bezier ale acestei suprafete trebuie memorate si cate pot fi recalculate pe baza proprietatilor de simetrie ?
- Care este reprezentarea in MATLAB a formulei de calcul pentru o BS cu ajutorul polinoamelor Bernstein ?
- Schitati o BS cu doua curbe de delimitare inchise.
- Fie polinomul p(x)=3x3+2x2-x+5. Scrieti acest polinom folosind baza Bezier.
- Calculati punctul unei curbe Bezier cubice, corespunzator valorii parametrului t=3/4 folosind algoritmul lui de Casteljau si polinoamele Bernstein.
- Punctele de control ale unei BC sunt : B0 = (64;0), B1 = (-64;64); B2 = (64;64) si B3 = (-64;0). Calculati punctul de pe BC corespunzator valorii parametrului t=1/3 folosind algoritmul lui de Casteljau si polinoamele Bernstein.
- Aceeasi problema pentru cazul in care punctele Bezier ale curbei sint : B0 = (-16;0), B1 = (-16;8); B2 = (8;16) si B3 = (16;0) si t=3/4.
- Se da urmatoarea curba (C) in reprezentare parametrica: x=4-t2, y=t3-t; t ∈ [0,1]. Calculati punctele Bezier ale curbei (C) si schitati curba (C) si poligonul ei Bezier.
- Definiti domeniul Voronoi al unui punct dintr-o multime de puncte M.
- Definiti diagrama Voronoi ale punctelor din multimea M.
- Definiti triangularea Delaunay.
- Desenati diagrama Voronoi si triangularea Delaunay a multimii de 3 puncte formate din varfurile unui triunghi echilateral.
- Desenati diagrama Voronoi si triangularea Delaunay a multimii de 4 puncte formate din varfurile unui romb.
- Desenati diagrama Voronoi si triangularea Delaunay a multimii de 4 puncte formate din varfurile unui patrat.
Puteti lasa si voi variantele voastre la aceasta materie, in comentariile acestei pagini.






