Testeaza-ti cunostintele la calcul numeric

1. varianta
1. Definiti eroarea absoluta si relativa a unei aproximatii β a marimii exacte x.
2. 1. Ce intelegeti printr-o metoda iterativa de rezolvare a unui sistem de ecuatii? Cum se asigura precizia dorita a solutiei in cazul metodelor iterative?
   2. Prezentati, la alegere, metoda Jacobi sau Gauss Seidel, de rezolvare a sistemelor de n ecuatii cu n necunoscute (Principiul metodei, algoritmul de rezolvare, conditii de aplicabilitate, conditii de asigurare a preciziei dorite).
   3. Exemplificati pasii metodei de rezolvare a sistemelor prin metoda eliminarii Gauss si rezolvati prin aceasta metoda sistemul de mai jos, folosind in rezolvare scrierea matriceala a sistemului.
      X1+2X2-X3+3X4=4
      2X1+4X2-X3+2X4=2
      -X1+X2+2X3-2X4=6
      3X1+3X2+3X3+6X4=10
   4. Folosind metoda injumatatirii intervalului (bisectiei), gasiti, cu o precizie de e <=0.1, o solutie a ecuatiei x3+3x-2=0.
3. 1. Definiti problema de interpolare Lagrange. Scrieti formula de interpolare Lagrange.
   2. Definiti polinoamele fundamentale de interpolare Lagrange.
   3. Scrieti polinoamele fundamentale Lagrange si formula de interpolare Lagrange pentru functia f, pentru care se cunosc urmatoarele informatii: f(-1)=3, f(0)=5, f(1)=10
   4. Calculati diferenta divizata pentru functia f de la pc. c) pe nodurile x0=-1, x1=0, x2=1: [x0,x1,x2;f]
4. 1. Ce aproximeaza o formula de cuadratura? Dati forma generala a unei formule de cuadratura si definiti elementele care apar in aceasta formula.
   2. Definiti gradul de exactitate al unei formule de cuadratura.
   3. Cum se obtin formulele de cuadratura de tip interpolator. Dati expresia coeficientilor unei astfel de formule.
   4. Calculati aproximativ
      
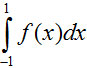
      pentru functia f de la punctul 3c).
   5. Presupunand ca pentru functia f se cunosc valorile pe oricate puncte avem nevoie, scrieti o formula de calcul a integralei de la pc. d) care sa ne permita obtinerea unei precizii dorite (o eroare prescrisa de noi).
2. varianta
1. Definiti eroarea absoluta si relativa a unei aproximatii α a marimii exacte y.
2. 1. Prezentati, la alegere, metoda Jacobi sau Gauss Seidel, de rezolvare a sistemelor de n ecuatii cu n necunoscute (Ce fel de metoda este, principiul metodei, conditii de convergenta).
   2. Exemplificati metoda aleasa scriind primele 3 iteratii ale metodei pentru sistemul
      X1+X2-X3+3X4=3
      2X1+X2-X3+2X4=4
      -X1+X2+2X3-2X4=6
      3X1+3X2+X3-X4=5
3. 1. Definiti problema de interpolare Lagrange. Scrieti formula de interpolare Lagrange.
   2. Definiti polinoamele fundamentale de interpolare Lagrange.
   3. Pentru functia f se cunosc valorile f(-1)= 3, f(0)=0, f(1)=2, f(2)=1. Ce grad va avea polinomul lui Lagrange pentru functia f, corespunzator acestor puncte. Scrieti polinoamele fundamentale Lagrange si polinomul Lagrange pentru f.
4. 1. Definiti o formula de cuadratura,elementele componente si gradul de exactitate al unei formule de cuadratura.
   2. Scrieti formula de cuadratura a trapezului, interpretarea ei geometrica si dati gradul de exactitate al formulei.
   3. Poate formula de cuadratura a trapezului sa aproximeze o integrala cu o eroare oricat de mica? Justificati folosind forma restului acestei formule de cuadratura:
      
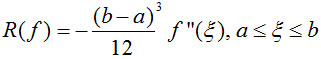
   4. Se presupune ca pentru functia f definita pe [-1,1] se cunosc valorile pe oricate puncte, xi, i=1,...,n . Scrieti formula repetata a trapezului pentru aproximarea integralei
      
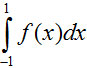
      Poate aceasta formula sa aproximeze cu o precizie data, ε, integrala? Justificati raspunsul folosind formula restului
      
      
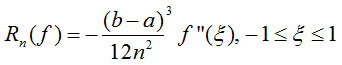
5. Scrieti la alegere, un algoritm care:
1. Calculeaza polinomul lui Lagrange de grad n, pentru functia f, pe punctele xi, i=0,1,...,n
2. Calculeza
   
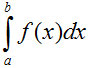
   folosind o formula de cuadratura repetata ( formula de cuadratura repetata a trapezelor sau a lui Simpson)
3. Rezolva un sistem de ecuatii folosind metoda lui Gauss.
4. Aproximeaza o functie folosind metoda celor mai mici patrate.
5. Calculeaza tabelul diferentelor divizate ale unei functii f.
6. Calculeaza diferenta divizata de ordinul n a functiei f pe punctele X0,...,Xn.
7. Rezolva cu o precizie data o ecuatie
Algoritmii vor fi scrisi modular, explicand semnificatia tuturor variabilelor folosite si comentand algoritmul.

Vedeti aici si alte variante.
Puteti lasa si voi variantele voastre la aceasta materie, in comentariile acestei pagini.